整数的表示和运算
最开始学习这些是在本科鼓捣单片机的时候,最近在看《深入理解计算机系统》,整理一下。
大端法,小端法
- 大端法: 最高有效字节在最前面的方式。
- 小端法: 最低有效字节在最前面的方式。
对于数字0x01234567:

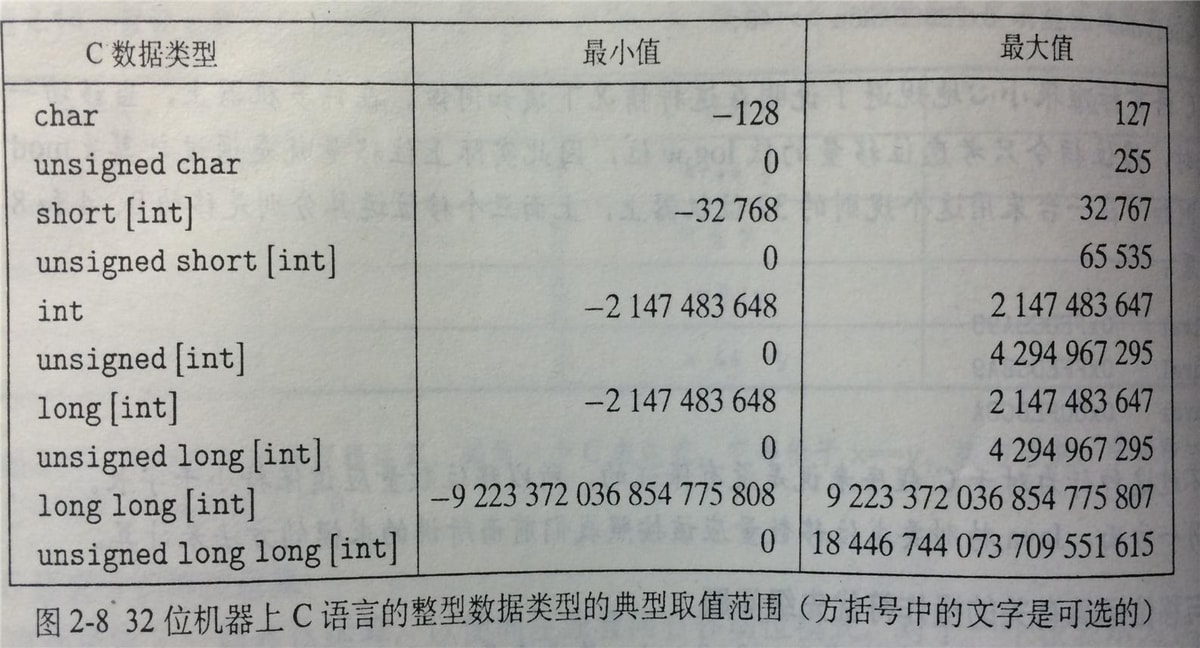
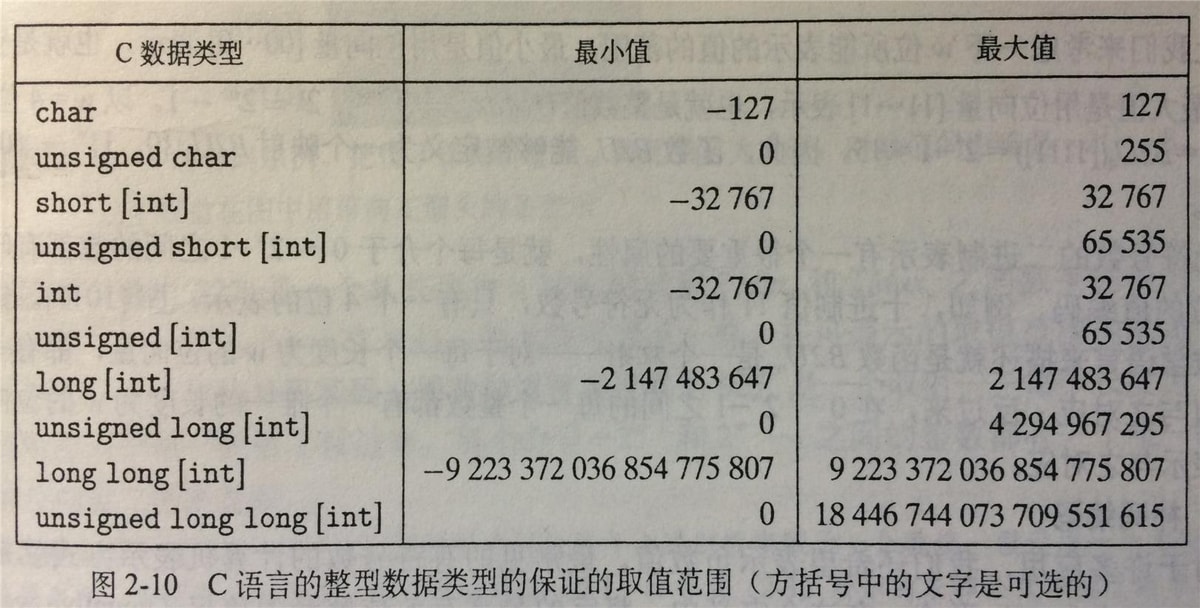
C语言中数字数据类型的字节数

运算符
- 位级运算:| 或、& 与、 ~取反、 ^异或
- 使用表达式~0可以生成全1的掩码,不管机器的字大小是多少,方便移植。
- 逻辑运算:||或、&&与、!非
逻辑运算的一个重要特性:如果对第一个参数求值就可以确定表达式的结果,那么逻辑运算符就不会对第二个参数求值。例如a&&5/a将不会造成被零除。(JavaScript 中可以用这种方法来提高浏览器兼容性:(functionA || functionB)(), 第一个函数不被浏览器支持时才用第二个函数。)
移位运算
逻辑右移:在左端补k个0。
算术右移:在左端补k个最高有效位的值。(几乎所有的编译器/机器组合都对有符号数使用算术右移)
整形数据类型

有符号数和无符号数
对大多数C语言的实现而言,处理同样字长的有符号数和无符号数之间相互转换的一般规则是:数值可能会改变,但是位模式不变。(保持位值不变,只是改变了解释这些位的方式。)
在执行一个运算时,如果一个运算数是有符号的而另一个是无符号的,那么C语言将隐式地将有符号数强制类型转换为无符号数,来执行这个运算。(特别是比较大小<、>时)
扩展一个数字的位表示
- 无符号:零扩展;
- 有符号:符号扩展。
1 | short sx = -12345; |
先要改变大小,之后再完成从有符号到无符号的转换。
整数的运算
无符号加法:计算和模上
2^w。(简单的丢弃x+y的w+1位表示的最高位来计算)s=x+y,通过s<x(s<y)来判断发生了溢出。补码加法:同无符号加法有相同的位级表示。
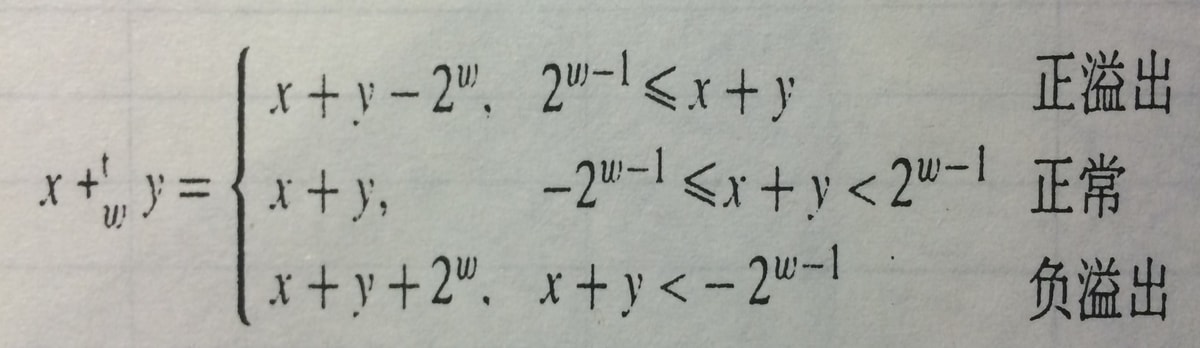
补码的非:
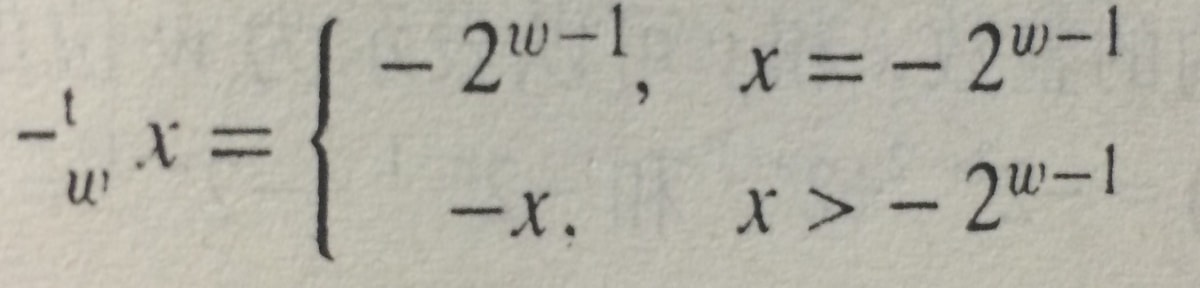
- 第一种方法:对每一位求补,再对结果加1。
- 第二种方法:假设k是最右边的1的位置,对位置k左边的所有位取反。
无符号乘法:整数乘积取低w位。
补码乘法:同无符号乘法有相同的位级表示。
乘以常数:转化为移位增加速度,例如:
x*14 = x*(2^4-2) --> (x<<4)-(x<<1)。
常数转化为二进制可以便于分解。
例如14:[(0…0)(111)(0)],考虑一组从位置n到位置m的连续的1(n>=m):- 形式A:
(x<<n) + (x<<n-1) + ... + (x<<m) - 形式B:
(x<<n+1) - (x<<m)
- 形式A:
除以2的幂
整数除法总是舍入到0,但移位结果总是向下舍入。例如-3.14应为-3,但移位得到的结果是-4;
因为:对于整数x和任意y>0,有⌈x/y⌉ = ⌊(x+y-1)/y⌋。
所以:右移之前先将x加上2^k-1。